前言
距离博客更新又是已经过去了一个月，本来要写的香港游记又不出意外地咕了。虽然看似我什么都没写，但其实我的大部分活动已经转移到memos了（毕竟用tg机器人发消息就是比网页更方便），当然也包括这门课的笔记。不过既然已经学完最后一节必修课了，且最后的几节课要记的内容也比较多，那么就拿到博客单独更新吧。
关于排序算法的补充说明
教授在讲到快速排序时提到了一个性质比较重要，那就是稳定性。对于稳定性的说明可以看这张图：
从这张图可以看出来，在经过序号排序后仍然能保持前面经过首字母排序时的相对位置不变，也就是箭头不会有交叉。而下面的案例则是不稳定的排序：
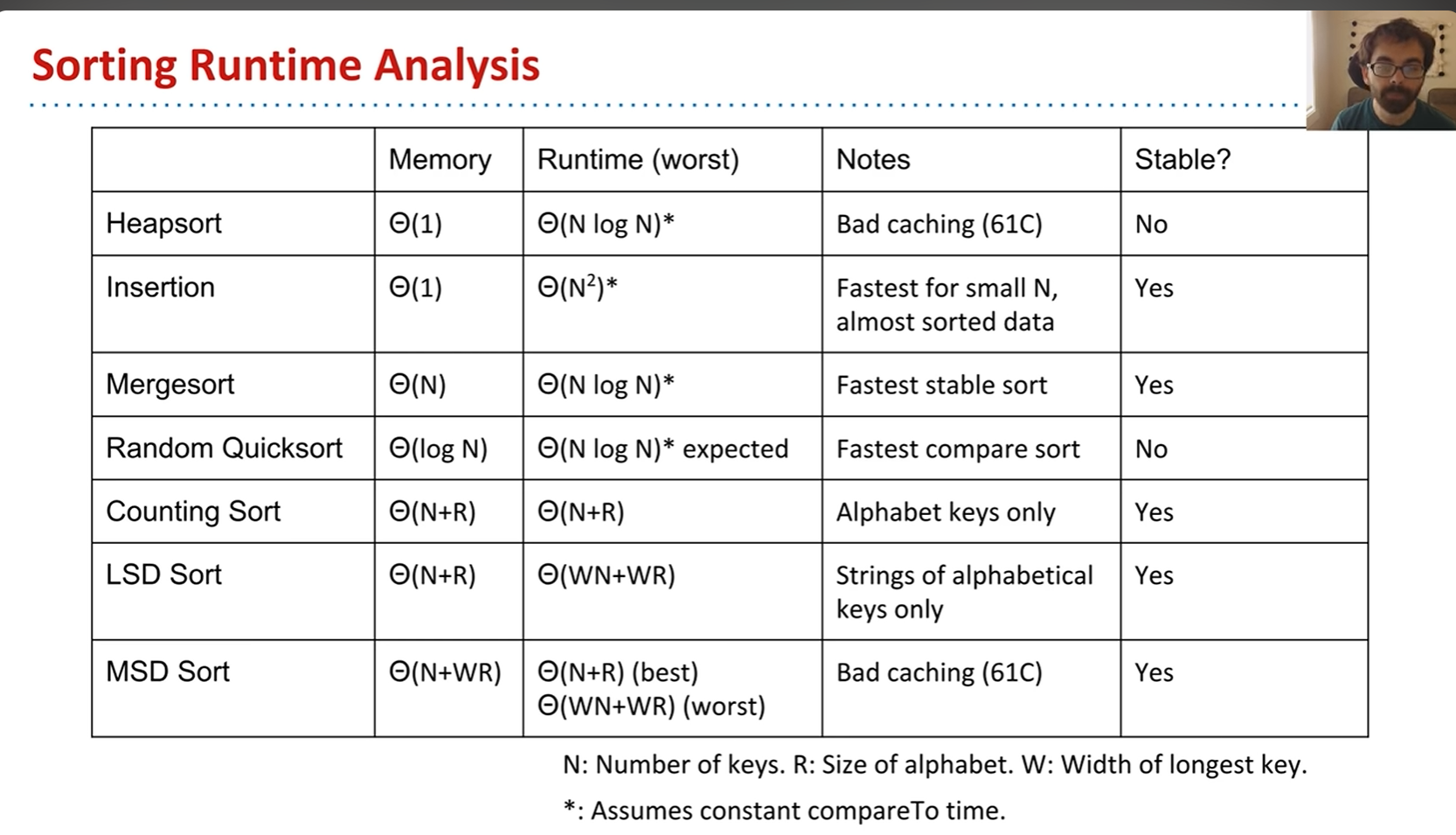
关于各种排序算法的稳定性可以参照这张图（下文提到的基数排序仍然是稳定的）
关于基数排序
计数排序
经过前面的"Puppy、Cat、Dog"游戏可以得知，基于比较的排序算法时间复杂度永远不可能小于O(NlogN)，但基数排序就能做到O(N)。下面是一个案例：
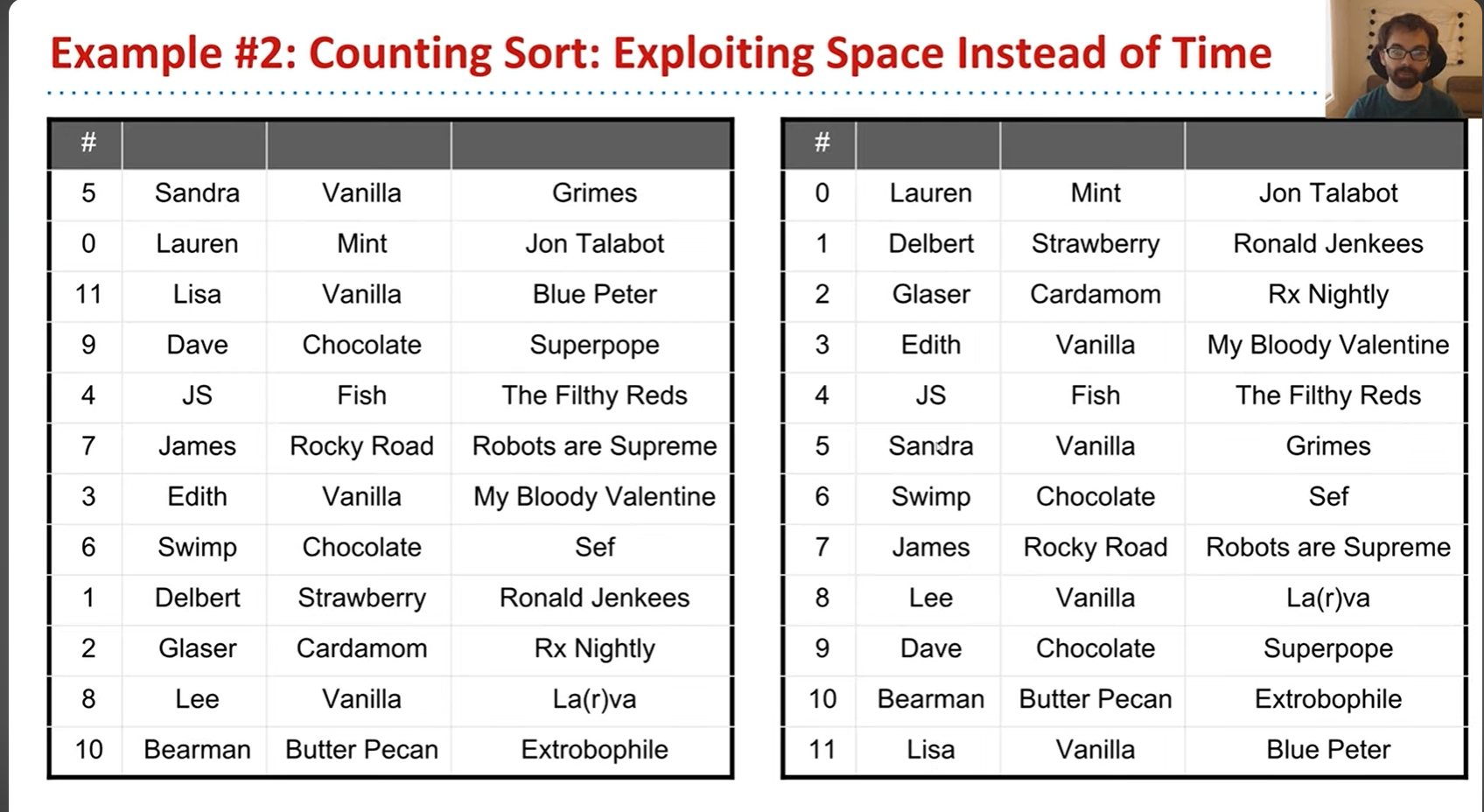
可以看出来实现方式很简单：只要新建一个数组，然后直接将序号作为索引插入数组即可。不过这么做缺陷也很明显：现实中是不可能刚好有这么整齐的序号的。因此还有另一种方法可以改进这一点：
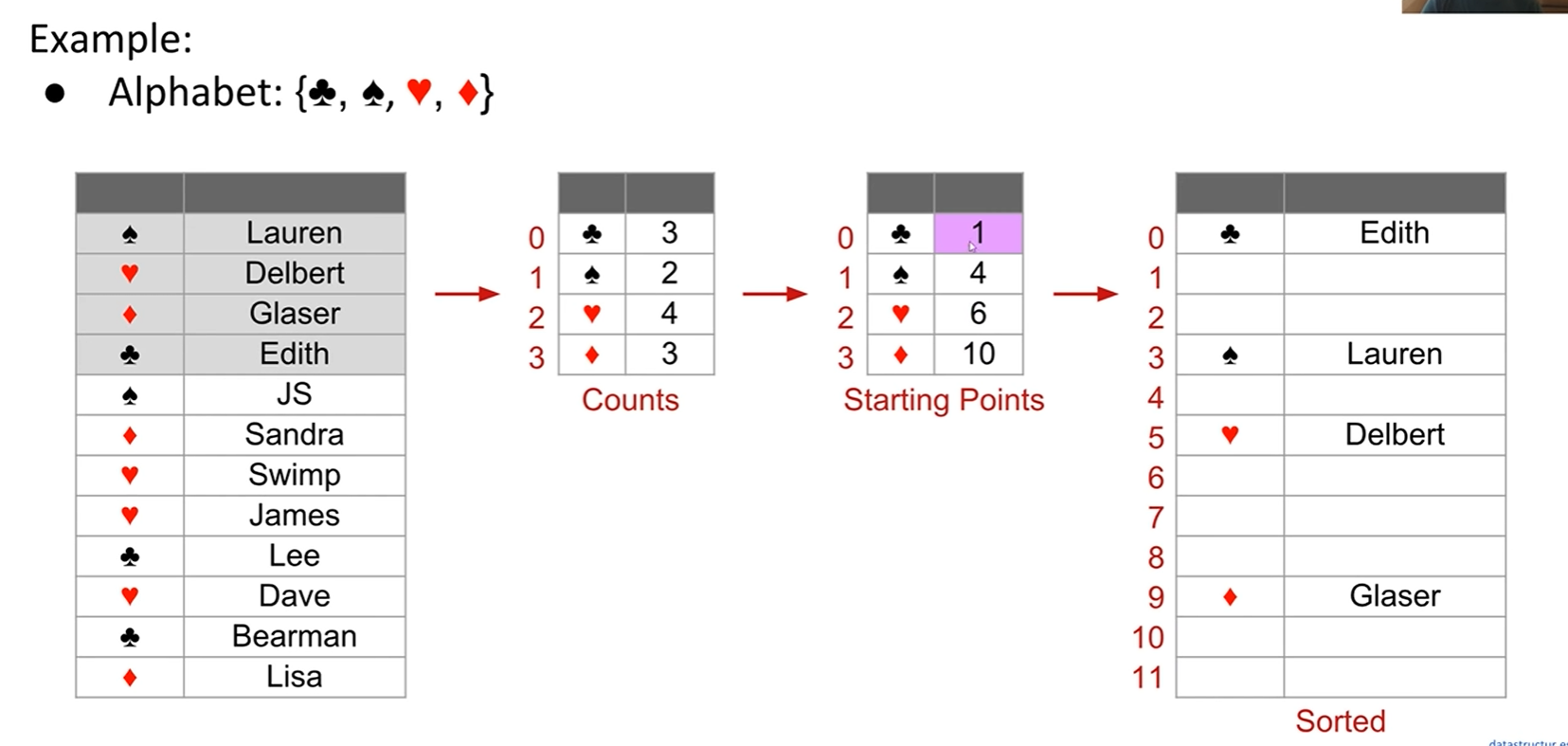
这是另一个示例，目的是根据字符表（这里是花色）将项目从大到小排序。实现方式一样很简单： 1.计算每一个字母分别有多少项，再通过这个新建一个起始表 2.根据起始表将元素插入新建的数组，每加一项就对起始表对应的数字+1 可以看出当起始表对应的数字增加到下一个字母表的起始点时该项正好能加完，并不会出现重复添加的现象。
但是这样做又有一个新的问题，那就是有的字符表太大了：
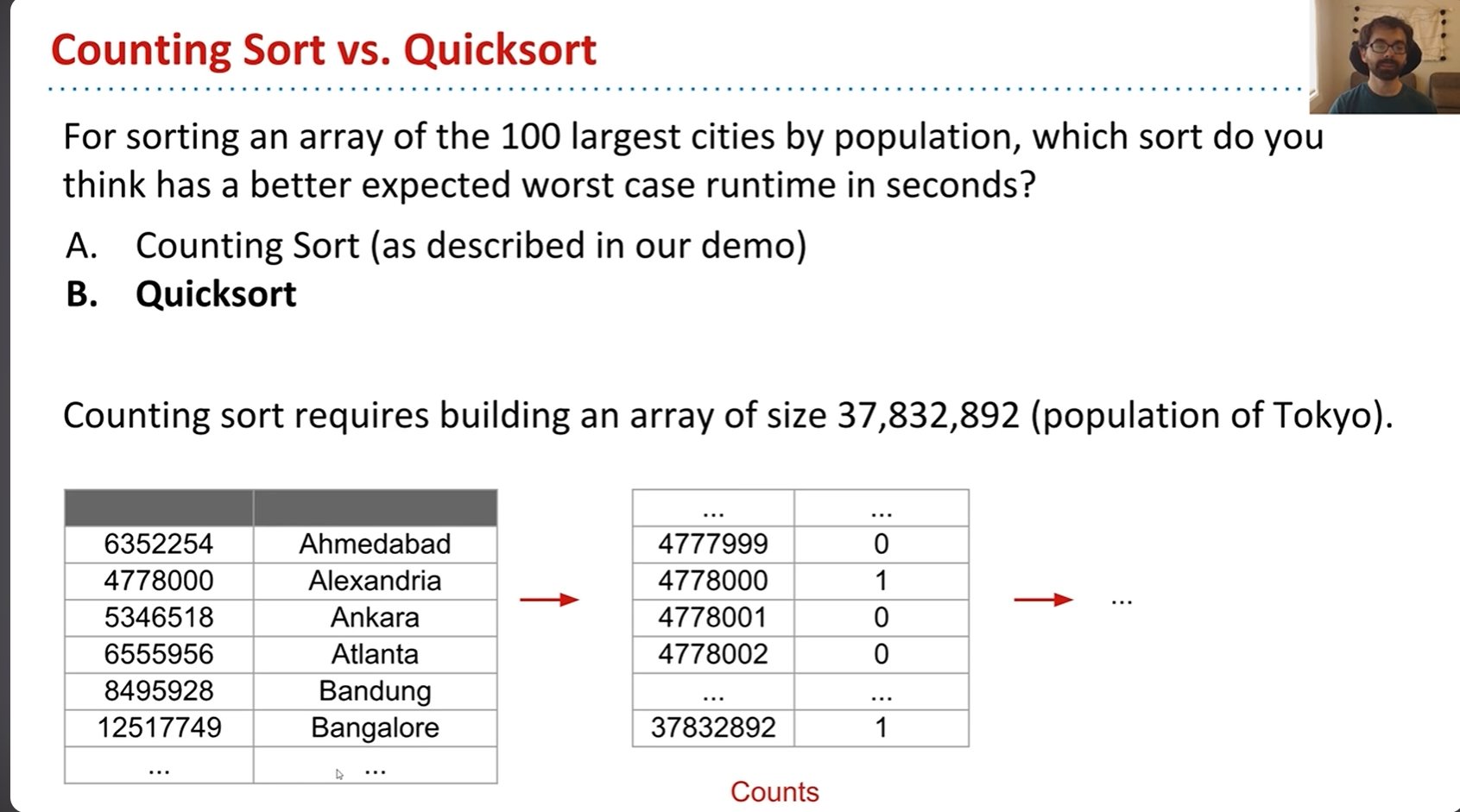
这是一个选出全世界人口最多的前100个城市的示例，可以看出如果想要做到这点就必须构建一个大小为3700万的数组，因为东京是一个拥有3700万人的大城市。假设N是数组的总数，R是字符表的个数，则时间复杂度是O(N+R)，N越接近R运行效率就越高，可以看出在这个示例中N是远大于R的。但这个问题也不是没有解决方案，那就是LSD和MSD。
LSD
这里的LSD当然不是指艺术家神药，而是Least significant digital的简称。这是有史以来最古老的排序算法，甚至能追溯到第二次工业革命，由美国自动制表人口普查所使用。下面又是一个示例：
总结起来其实就一句话：从右往左排，也就是先对右边的数进行计数排序，再向左一个个排。如果位数不够就在空白处用点代替，然后向上或向下移动。时间复杂度为O(WN+WR)，W为最长的字符的长度。
MSD
LSD看起来似乎已经够完美了，但让我们再来看一下以下情况：
这四个字符都是英语最长的单词，意思是什么不重要，但当我们试图通过LSD进行排序时，我们需要从右往左遍历所有字符才能对其进行排序，即使我们知道只要对第一个字母进行排序即可。那么有没有解决方案呢？当然有：从左往右排。但MSD所做出的改进并不止如此，再来看一个示例：
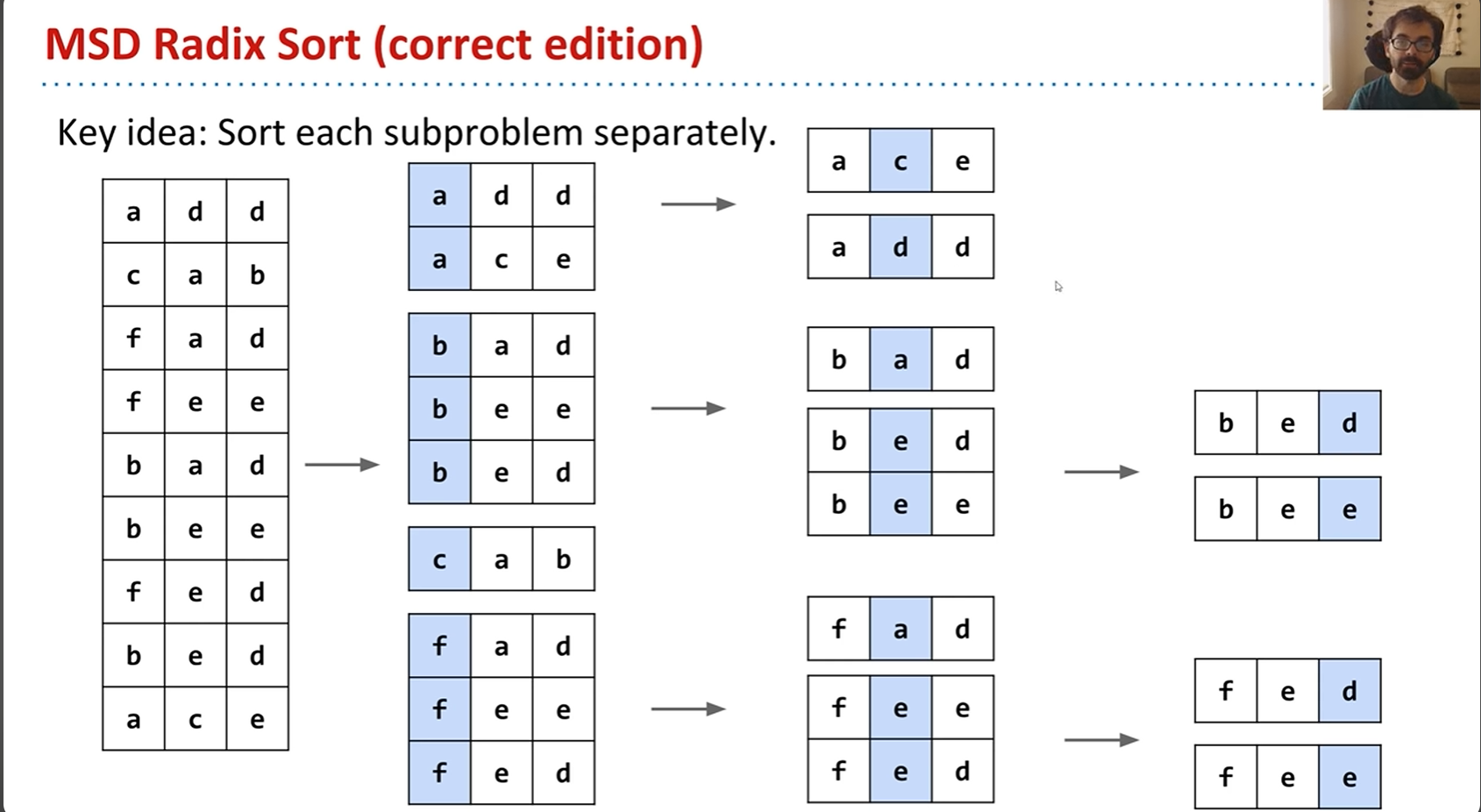
这是另一个MSD的示例，后面懒得写了，放一张图作为最后的总结吧：
最后还提到了JIT这个东西，并详细介绍了如何优化程序的运行速度，这里就不展开了，笔记到此结束。
后记
第一次知道这门课还是在知乎以及csdiy.wiki上，当时我也是三分钟热度，看到这门课适合有编程基础的人群时便稀里糊涂地选了这门课。然而还是受三分钟热度影响，我学这门课一直磕磕绊绊地学了半年，中间也咕了很长一段时间，而北大大佬几乎在一个月内就学完了，只能说人与人的差距比人与狗还大。这是我第一次真正接触纯英文教学，虽然前面还得挂字幕才能看懂，但在今天刚开始时字幕有问题，我便尝试不使用字幕听课，竟然也能听懂大部分内容，可以说明我的英语听力水平也在这门课中提高了不少比学校的半吊子国际课程好多了。这也是我第一次感受到纯念ppt和结合实际讲课的差距，Hug教授的课程给我留下了极深的印象，希望以后还能有听课的机会。虽然后面软件工程的内容都是选修课程，我并没有听完，proj3也因为没有学伴而无法完成其实就是太蔡了怕麻烦，但前面所学的数据结构与算法的相关内容以及做过的proj1和2也是我翘课的最大底气了。正好上学期买的csapp一直都没动过，那么之后便向61c继续努力了，争取把计算机组成原理和网络都学完，这样大概率就能在班里横着走了，也能少受点教室里来自老师的折磨。
那么就这样吧，明天开始学习61c，顺便把数学不懂的地方补完什么补完计划，向083500前进。
2023.11.1